I'm a practical person. When I look to the future I know that fusion drives are cool, and that general relativity is awesome, and that genetic engineering is whiz bang. But after my 10th cup of coffee contemplating these matters, I need to place that excess fluid I've built up somewhere.
Science Fiction is notoriously bad about bathrooms. I challenge you to find Men's room sign in Star Trek. Star Wars has data ports and plasma conduits and cryogenic freezers. But have you ever seen something that resembles a washroom?
I used to work at a science museum. It was a fascinating old building that was built for a fascinating old time. A time where thousands of square feet in galleries could be serviced by a bathroom with one stall each for gents and ladies. We spent nearly as much effort and budget bringing bathrooms up to modern standards during renovations as we did on the exhibits themselves.
Toilets are a modern day magic. People use them. People have mythologies about them. But how many people know how they actually work? And if you brought Benjamin Franklin back from the dead, how amazed would he be by its operation?
Now in standard science fiction, facilities like food service and bathrooms are relegated to space magic. The author didn't feel like getting into the details, so don't ask because stuff is just taken care of. If the plot doesn't call for some difficulty in a lavatory, they just leave the lavatory (and the physics for how it works) out.
But for me, that's not good enough. And it's because I've spent years studying the insides of buildings and the insides of ships. I know how much work has to go in behind the scenes to pull off magic like toilets. I also know that various systems that try to replicate their function can be really horrible. I also know that things going wrong in the magic plumbing world can have dire effects in the non-magic world. For instance the loss of U-1206 The events of it's demise were set off by someone not understanding how to operate the high-tech toilet on board.
The issue is coming up because I'm finding problems designing the shape of a deck that will allow water to drain properly in the artificial gravity system I am also designing. I touched on the issue in my prior post: On the Curvature of Decks. Today I'm actually trying to understand the problem from the toilet's perspective.
To do that we need to understand exactly how a toilet actually works.
A toilet is a siphon. When you pull the handle, 1.5 gallons of water dump into the bowl at once. This causes water to fill up a tube with liquid that was formerly filled with air. That full tube of liquid then wants to pull all of the water in the bowl with it to the sewer. With the liquid gone, the tube fills with air again, and we break the siphon. A filler than fills the toilet bowl back up to the level high enough to catch feces, but not high enough to flush.
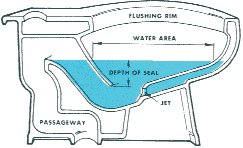
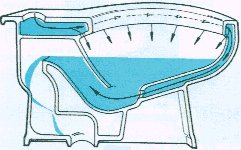
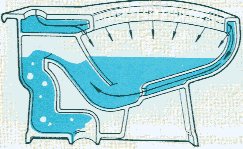
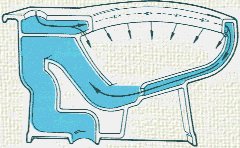


Images Courtesy of https://www.physics.hku.hk/~phys0607/
I just tested the process on a toilet here at the office and the entire flushing process was over in 5 seconds, but I'm pretty sure the siphon only lasted for the last second of it. Flushing 1.4 gallons of water in 1 second gives a peak flow rate of 1.4*60 = 84.0 gpm.
It turns out there are all sorts of charts and tables and guidelines on the subject of properly sizing drain pipes. So I'm going to estimate that we probably have a 4" line run into the office.
There is a lot of "and the world accelerates everything downward at 9.8m/s/s" that is baked into plumbing science. Gravity provides accelleration. Accelleration plus mass provides force. But on the Iliad we have two different modes for "gravity."
When the ship is thrusting, the engines provide 9.8m/s/s of accelleration. That mimics gravity on the Earth perfectly. However, what if the engine is off? What if we need to operate at 10% for a particular maneuver?
When the engines are not running at full thrust, the habitat area of the vessel rotates. The speed of the rotation at a full stop is enough to provide 1 g of centripetal force to someone standing at the 1 g radius. However, for the decks "below" the 1g level, there is more force. Of the decks "above" the 1g level, there is less force. In addition to the centripetal force, there is are Coriolis forces. The top of an object is pulled backwards from the direction of the rotation. This also applies to fluids. We see the phenomena on Earth, Coriolis forces actually cause "hills" to form in the ocean. On our ship, we well see containers of water pile fluid on one side.
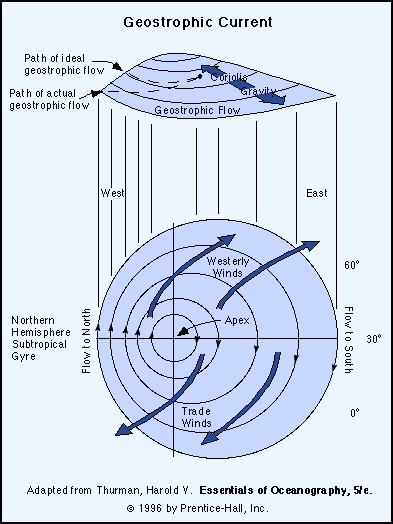
Supply pipes are normally full of water, so this effect can be ignored, but drainage pipes are only ever allowed to be half full. Depending on what direction that are in relation to rotation, water could flow in strange ways:
Running a drainpipe in a way that the flow runs counter to the Coriolis forces will introduce turbulence and reduce the flow. Running it in the same direction as Coriolis forces will increase flow.
So one quick ruling we have is that drain pipes must ALWAYS be run in the same direction as Coriolis forces. If for whatever reason we have a pipe that needs to be run opposite of Coriolis forces, the capacity of those pipes need to be uprated, or demands downrated, to account for a drop in flow.
For floor drains, we don't actually care about the slope of the deck itself. We care about the slope of the section of floor. And if we want to make sure that water drains properly we need a drain in the lowest part of the floor (for accelleration) and a drain in the spot where Coriolis forces are going to drag the water. If we can make the two the same, even better. There are going to be other oddities though. Take a shower stall for instance:
Assuming we get the drain in the right place, we actually need either two shower heads installed, or one of those wands with a hose. The path water will take out of the nozzle is going to be very different between accelleration and rotation mode. And wo betide the homeowner who discovers their shower was installed backwards! When I was working out the flow of water I also found that we may need to slope that back wall to scoot water in the direction we want it to go.
As you can imagine, the direction a toilet is installed matters too. But there simply taking a standard toilet and installing it just so won't cut it. We need a slight design tweak from its Earthbound cousins. Toilets on board will have to ac-commode-ate (heh) the fact that the siphon threshold will be different in the two modes.
Though odds are there are going to need to be more modifications than that to handle situations where gravity is lost completely. We don't need them to work in zero G. But we also don't need to flood the ship with water because the float that controls the tank fill is...well...floating. It'll also probably have to have a way to lock the lid to keep the drains from filling the compartment with sewage floating up through the water trap that, oddly enough, doesn't work when there is no weight at all.
Given that we have a lot of tailoring to do to our various fixtures (even if the design principle works), perhaps we should start back over with a simpler flat deck and sort out if the pitch of the floor is our most pressing concern. To do that I need to calculate what is actually the magnetude of the Coriolis effect for various levels on the ship, and then compare that to the other forces at play (for instance, weight).
Part of the challenge is that most of my exposure to the concepts of the Coriolis forces are from high-speed, low radius experiments and demonstrations:

And oddly enough, old school plumbing tables (some of which go back as far as the Romans) can help. Human-kind has been channelling water through pipes for thousands of years. Before we had calculus to describe fluid flow, people just sat down and experimented until things worked. One useful concept is Hydraulic Head.. Essentially, there is a relationship between pressure and difference in height, all other factors cancelling out. And then, in our infinite wisdom, people sat down and scrawled out various data tables to describe all of those other factors.
I have to be careful because all of these tables are English units that take constant accelleration due to gravity as an assumption. So after I do all of my Coriolis effect math on the 1g level (at 500m), I next have to correct for changes in centripetal accelleration and weight for the levels above and below the 1g level. Note I said weight. The mass of water will not change. But the force exerted by gravity (accelleration or rotational) does change. 1 liter of water will always have mass of 1kg. But it's weight in pounds will change from 2.2lbs on the 1g level, to 0.88 pounds on the 320 level (where the rotational radius is 180m and gravity is 0.4g).
The equations to describe forces acting on a system in rotation are: (reference Coriolis force)
This force is applied to things that are moving along a rotational body. The X is the equation is NOT scaler multiplication. It is the cross product of a vector. (i.e. the inputs are vectors and the output is another vector.)
Behind the scenes we are seeing three different forces/effects described at once:
The soup of letters in those equations mean:
is the rotation vector, with magnitude ω of the rotating reference frame relative to the inertial frame
is the vector sum of the physical forces acting on the object relative to the rotating reference frame
is the velocity relative to the rotating reference frame
is the position vector of the object relative to the rotating reference frame
is the acceleration relative to the rotating reference frame
Determining if difference in weight is actually a problem on flat decks
Before I go whole hog into vectors and whatnot, what is the magnetude of some of these forces, and are they enough to overcome other effects in plumbing equations?
The first term the cancels out is . For the moment we will ignore external forces
acting on the water. The second term that cancels out is the Euler Force. That only applies
if the rotation itself is changing speed. The Centrifugal force is actually our placeholder
for weight in our equations. So all we are left with, in the end, is identifying case where
the Coriolis force overcomes our Centrifugal force.
And that only seems to happen if our velocity is in the direction of rotation. If our velocity is in the opposite direction than that or rotation we actually pick up apparent weight.
Now let's have a look at our flat deck concept, currently I have most of the housing, offices, and factories concentrated around that equator of the sphere. This is not actually at the 1g radius, but 135 meters short if it. On that level the center of the deck would receive 0.77g. If the deck was flat and level, the outside areas of the deck are at a slightly increased radius. The deck at that point extends 163 meters in either direction, the Centrifugal accelleration on the outermost point is 0.84g:
Water moving through a pipe along the deck is going to experience a Coriolis force. If we cancel out the mass, we can also express that factor as an acceleration. To do this, though, we need to express the velocity of the water. If we consult our handy pipe schedule velocity chart, a standard toilet flushing 80gpm through a 4 inch pipe moves through the pipe at 2.04 feet per second (0.621 m/s), AND experiences enough friction to counter .81 feet of drop over 100 feet of pipe. Ignoring friction for the moment, a mass moving at 0.621 feet in the direction of the ring's rotation at 385m from the center experience an accelleration of (0.621 * 2 * 0.14)/9.8 => 0.02g. The 0.14 is the angular speed of the ring, which is rotating at 1.34 RPM.
Translation: I can pretty much ignore the Coriolis effect. Though we still have the problem with flat decks because the difference in Centrifugal accelleration between the outer deck and inner deck means water is still trying to flow, essentially uphill between the rightmost point of diagram above, and the center. Conversly, the water would have a downhill flow from the center to the left. But.. by how much? Water in the pipe is moving as it leaves the toilet at 0.621 meters per second. It will travel the 164 meters from the outside of the deck to the center in 264.1s. If we had built our drain pipe to code as a building, and we put our drain in the center of the deck, it would have a slope of at least 1/4 inch in the vertical per foot in the horizontal, which in metric would be a drop of 0.02 meters vertical per meter horizontal. Which would mean our drain connection is actually below the center of the deck, in this case 3.417m down.
Oops. When I designed the deck system originally, I had accounted for 1 meter of "utility and structure go here." Now it seems I need to either allow for 3.5 meters or I need to build at least that much slope into the deck, naturally. We also have the option of increasing the slope as high as 3 inches per foot (0.00 dy/dx). Which could make the outside of the deck up to 41.0 meters higher than the inside.
If we plot those slopes we see the following:
The purple line is the maximum slope allowed while under constant accelleration, the black line is the minimum slope allowed while under constant accelleration. The grey line is the original flat deck. None of this is fitting into the nice confines of the structure I had in mind. At all.
But then my mind turned to "How are homes built?"
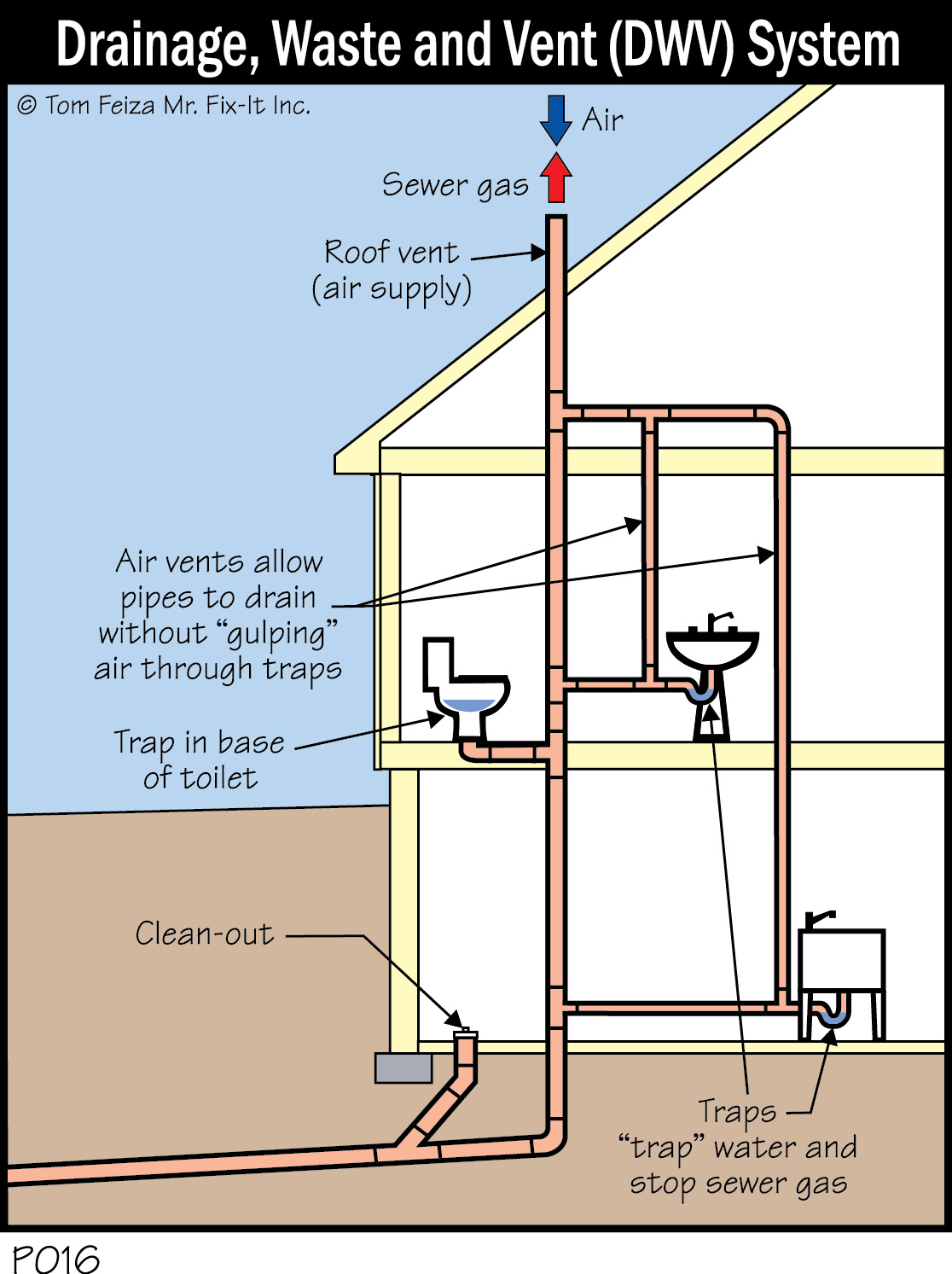
And one immediate feature that should pop out: vertically. Buildings are constructed up. This ship has a lot of vertical room. And I also had to harken back to my days in the Museum. If you've ever seen the movie The Matrix there is a scene where the characters are escape by making their way through what is in the movie is called a "wet wall."

The Franklin Institute also had structures like these. Almost two meters across, and running straight down to the foundation. It was where pipes and ducts could run without intruding on the galleries. (As the network guy, I occasionally had to trace a cable through there.) Strategically placed, these "utility zones" could run the entire height of the sphere, if need be. Though there is also a school of thought that says make the hallways wider, and just disguise the utilities with cover plates.
I also, thankfully, ran a spare deck below each of the settled areas that was already earmarked for utilities. And there are three decks at the bottom of the sphere I had originally envisioned as a reactor room, but I can now see better as a water treatment plant. We'll just shift the power production out to a main engineering area, and that also prevents any opportunity for heavy water isotopes to be introduced into the municipal water system.
The cut-outs needed for all of this utility access don't actually present a large enough footprint that we couldn't just treat them as part of the passage or part of the compartments they serve. But... I can make the player aware of its presence in the hallways, and if the plot should call for it, we can stage various utility emergencies to happen in the appropriate places.
Long story short... running drainage pipes vertically will solve the problem of how to properly drain a toilet in artificial gravity. Because Coriolis forces are small given our enormous radius and slow rotational speed, we can eliminate those as a consideration so long as we keep our horizontal pipe lengths reasonably short. (Less than 100m or so). With the current layout, no part of a compartment is ever more than 40 meters from a passageway, so passageways can act like the streets of our city, with people walking above, and utilities running below.
The only real design "gotta do" is to keep the layout for the settlement consistent for all three decks, to allow some utilities to stack. Each office, factory, and home is probably going to have a small carve out to carry drainage from the spaces above to the utility spaces below.
I can also eliminate having to put a special slope on decks. Any inhabited space or street is going to have floor drains placed periodically throughout. There is no special need to have those drains be anything other than slightly lower than the surrounding floor.
Although... we still are going to need to specially design the showers, and sinks really should always face away from the direction of rotation. This is because while water leaving the faucet will start off with a velocity that will carry it to the floor or bowl, if it splashes it will be weightless and float until the wall comes up to meet it in rotation.